2018年12月10日应我院张跃军教授的邀请,美国堪萨斯大学(University of Kansas)经济系张建波教授来我院举行题为《多方讨价还价的博弈问题》的学术讲座。张建波教授于宾夕法尼亚州立大学获得博士学位,现任教于美国堪萨斯大学经济系。主要研究领域为博弈论、微观经济理论、信息经济学和金融资产定价理论。目前已在Economic Theory、Journal of Mathematical Analysis and Applications等国际权威期刊发表论文20余篇,获得“迈克尔经济学创新研究奖”等5项重要科研奖励,在进化博弈方面的研究,已得到全球281个专业引用。
该讲座主要介绍了张教授团队开发建立的针对二人以上(多人)的博弈模型。
背景介绍:
影响博弈均衡的四大元素包括策略空间、支付函数、决策程序、信息结构。
Rubinstein—Stahl讨价还价模型主要应用于二人之间的讨价还价博弈模型,涉及此类问题时,也需要大量的计算。涉及多人之间的讨价还价模型时,Rubinstein—Stahl难以适用。

(二人博弈Rubinstein—Stahl模型公式)
针对这一问题,张教授团队开展了以下工作:
1,针对参加博弈成员以及整个博弈过程定义了博弈的操作者
Define bargaining operators for each player and for the game.
2,在考虑以每一个博弈成员的份额作为博弈中的测量标准,建立了一个基于博弈操作者的马尔可夫链
Generate a Markov chain based on bargaining operators, regarding shares for each player as a measure of the game.
3,该独有的变量测量标准是此博弈中独有的平衡,即该博弈中的特征向量
The unique invariant measure is the unique equilibrium of the bargaining game, which is the eigenvector associated with the unitary eigenvalue of the bargaining operator of the game.
4,建立了一种新的Rubinstein—Stahl平衡模型,该模型针对不同的因子,解决了之前的难题。
Generalize Rubinstein—Stahl model of bilateral bargaining to multilateral bargaining with different discount factors, circumventing intractability problem in backward induction.
5,建立了无秩序多人博弈平衡模型
Generalize to multilateral bargaining with random transition of moves.
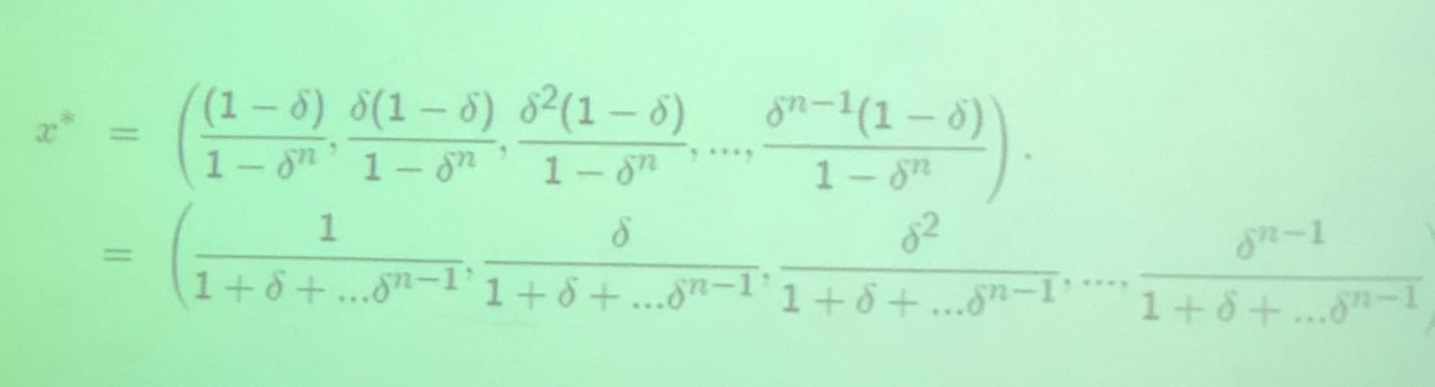
(有秩序多人博弈平衡模型)

(无秩序多人博弈平衡模型)
供稿:李华


